강의노트 22. 자료구조 - tree(트리), heap(힙)
19 Apr 2017 |패스트캠퍼스 컴퓨터공학 입문 수업을 듣고 중요한 내용을 정리했습니다. 개인공부 후 자료를 남기기 위한 목적임으로 내용 상에 오류가 있을 수 있습니다.
tree (트리)
- 참고글
- 그래프와 함께 비선형 자료구조 의 일종으로 계층 구조 를 갖고 있는 자료구조 (선형 자료구조 : 리스트, 스택, 큐)
- 트리의 주 목적은
탐색 - 이진 트리(binary tree) : 최대 2개의 자식 노드를 가질 수 있다.
- 완전 이진트리 (complete binary tree)
- 포화 이진트리 (full binary tree)
- 사향 이진트리 (skewed binary tree)
- 트리를 표현하는 용어
- 차수(degree, 특정 노드의 자식 노드의 수)
- 높이(height, 루트 노드에서 단말 노드까지의 깊이)
- 레벨(level, 각 층의 번호-루트노드:레벨1)
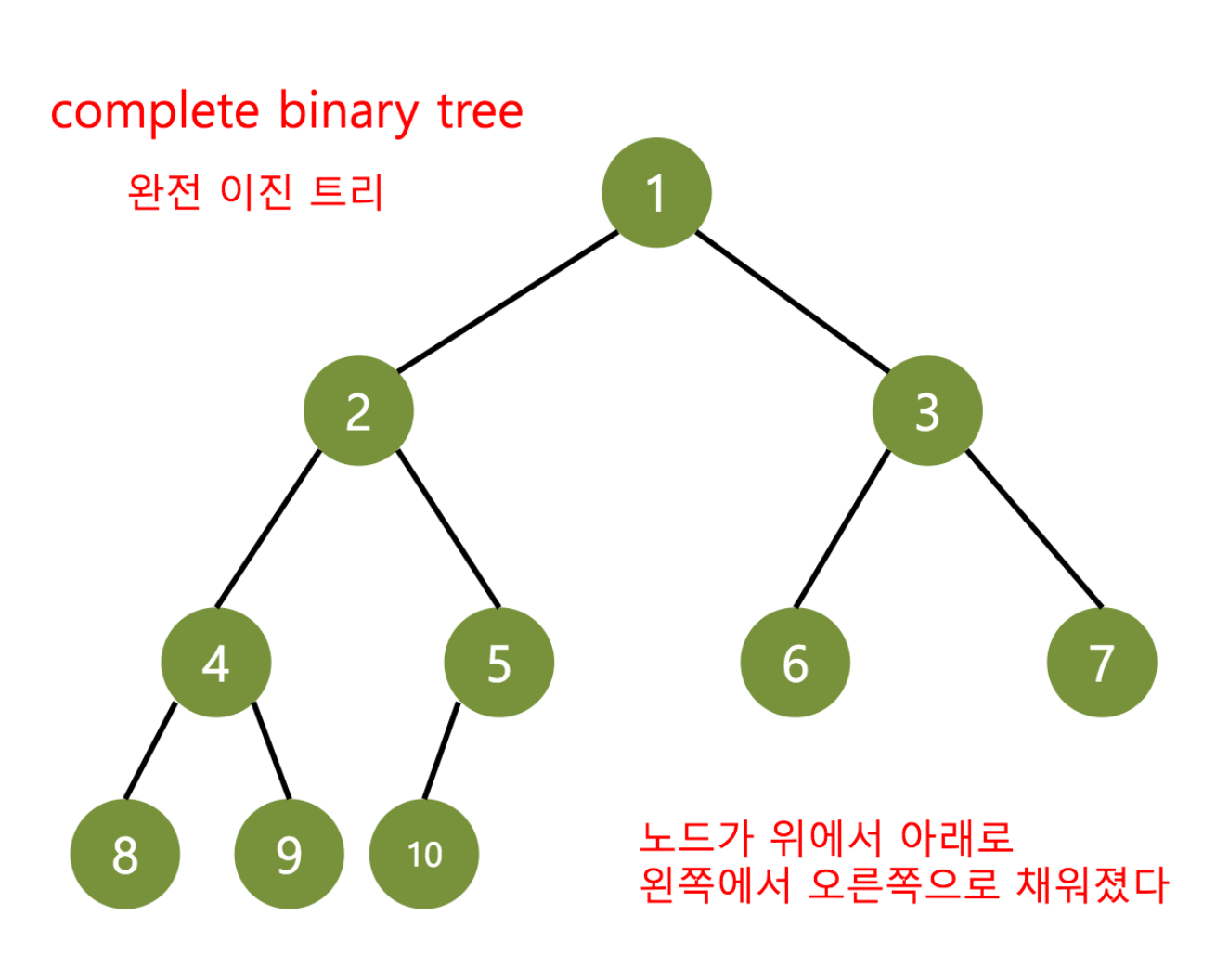
complete binary tree (완전 이진트리)
- 노드가 위에서 아래로, 왼쪽에서 오른쪽으로 채워진다.
- 잎 노드 두개의 레벨 차가 1 이하이다.
- heap 구현시 완전 이진트리를 기본으로 하며, 전통적으로 배열을 이용해 구현한다.
heap (힙)
- 참고글 - 최소힙에서의 추가, 삭제
- 수업자료
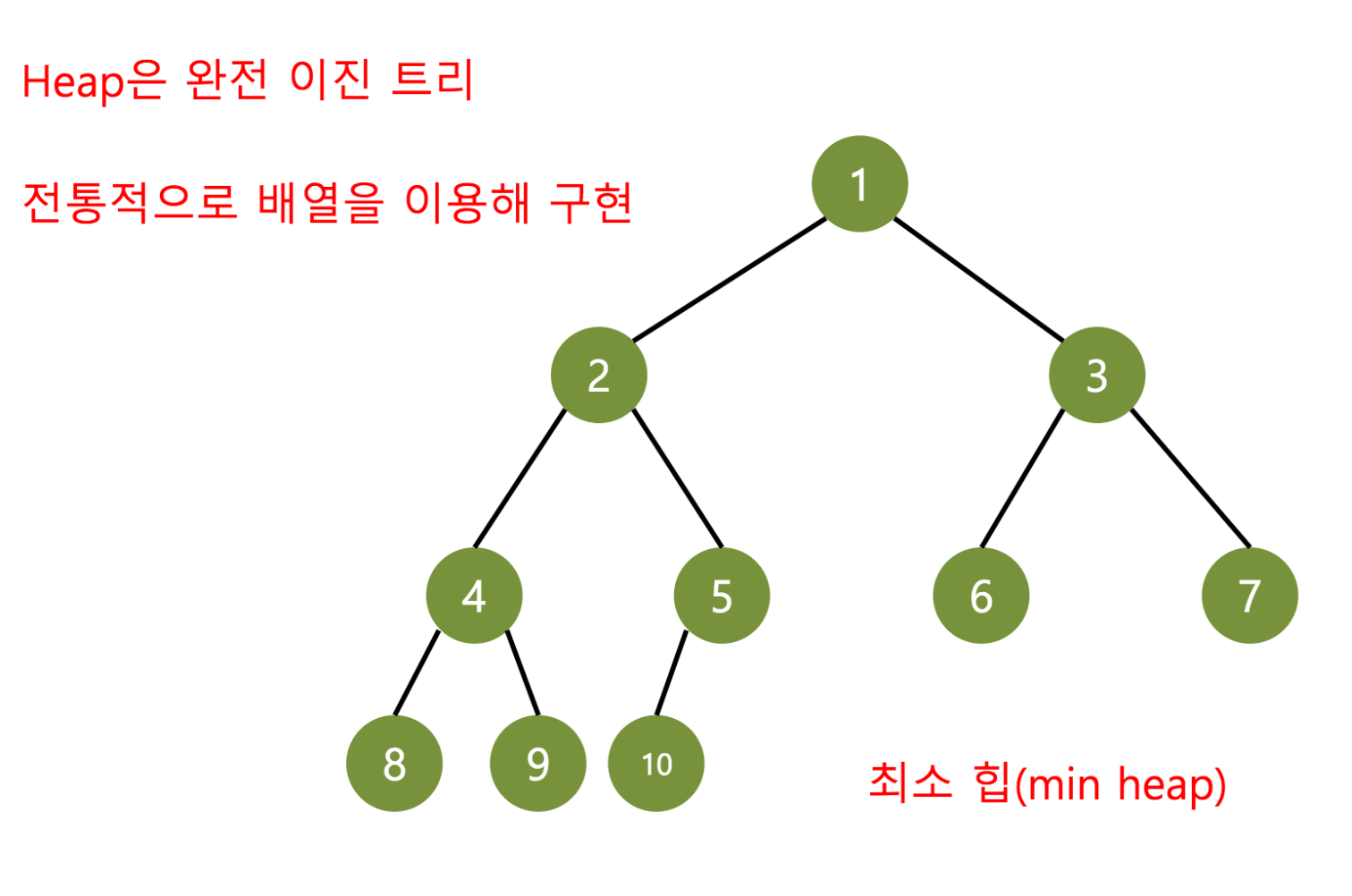
- 힙(heap)은 완전이진트리(Complete binary tree)를 기본으로 한 자료구조(tree-based structure) (시간복잡도 : O(log N))
- 일반적으로 배열을 사용하여 구현한다.
- 완전이진트리는 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안
- 다음과 같은 힙 속성(property)을 만족한다.
- A가 B의 부모노드(parent node) 이면, A의 키(key)값과 B의 키값 사이에는 대소관계가 성립한다.
heap의 종류
- 최대 힙 : 부모노드의 키값이 자식노드의 키값보다 항상 큰 힙
- 최소 힙 : 부모노드의 키값이 자식노드의 키값보다 항상 작은 힙
- 키값의 대소관계는 오로지 부모노드와 자식노드 간에만 성립하며, 특히 형제 사이에는 대소관계가 정해지지 않는다
heap 구현
index
- One based index heap
- 루트노드 index로 0이 아닌 1을 지정하여 구현을 좀 더 편하게 할 수 있다.
- parent index = child index // 2
- left child index = parent index * 2
- right child index = paretn index * 2 + 1
insert() 구현
- 맨 마지막 노드에 새로운 데이터 추가 (완전 이진트리 유지 - 최고 깊이에서 가장 오른쪽에 노드 추가)
- 부모 노드와 비교, 최소 힙 인 경우 부모보다 신규 노드가 작다면(우선 순위가 높다면) 교환
- 반복하여 부모 노드와 비교
- 루트 노드에 도달했거나 (부모가 없음) 부모 노드가 더 작거나 같다면 멈춘다.
delete() 구현
- 루트 노드를 반환 (최소 힙에서 최솟값을 뽑아낸다는 건 루트 노드를 뽑아낸다는 것과 동일)
- 맨 마지막 노드를 루트 노드로 이동 (A)
- 두 자식 노드를 비교해 우선 순위가 높은 것을 선택 (최소 힙인 경우 작은 수) (B)
- A 와 선택된 자식노드 (B) 를 비교하여 우선순위가 높은 것을 부모노드로 이동
- 반복하여 자식 노드와 비교
- 터미널 노드에 도달했거나 (자식이 없음) 자식노드가 더 크거나 같다면 멈춘다.
배열을 사용한 heap 구현코드
class Heap:
# 개체들이 공유하는 메소드는 클래스 메소드로 만들어도 된다.
def get_parent_idx(self, idx):
return idx // 2
def get_left_child_idx(self, idx):
return idx * 2
def get_right_child_idx(self, idx):
return idx * 2 + 1
# 중요함수- 보통은 유저 프로그래머가 직접 구현, 인터페이스만 제공
# 우선순위에 따라 반환값이 달라진다.
def get_prior(self, value1, value2):
'''
value1 이 우선순위가 높으면 -1 리턴
value2 가 우선순위가 높으면 1 리턴
두 우선순위가 같다면 0을 리턴
'''
# min_max == 1 ==> 최소 힙
if self.min_max == 1:
if value1 < value2:
return -1
elif value1 > value2:
return 1
else:
return 0
else: # self.min_max == 2 ==> 최대 힙
if value1 > value2:
return -1
elif value1 < value2:
return 1
else:
return 0
def __init__(self, s_min_max = 'min'):
self.dynamic_arr = [None, ] # one based index, 다른 언어는 가변배열을 사용한다. C++은 백터 사용, 효율 좋게 짜는 것이 중요(가변배열이 수정시마다 매번 탐색, 복사, 삭제를 하면 메모리 낭비)
self.num_of_data = 0 # 마지막 데이터의 index
if s_min_max == 'max':
self.min_max = 2
else:
self.min_max = 1
def is_empty(self):
if self.num_of_data == 0:
return True
return False
def size(self): # ADT에 없는 함수이지만 테스트용으로 만듬
return self.num_of_data
# insert 메서드에서 사용
# 부모 값과 비교해서, 우선순위가 부모 보다 높으면 True 낮으면 False
def is_go_up(self, idx, data):
if idx <= 1:
return False
parent_value = self.dynamic_arr[self.get_parent_idx(idx)]
if self.get_prior(parent_value, data) == 1: # 부모 우선순위가 작다면
return True
else:
return False
def insert(self, data):
if self.is_empty():
self.dynamic_arr.append(data)
self.num_of_data += 1
return
self.dynamic_arr.append(data)
self.num_of_data += 1
idx_data = self.num_of_data
while self.is_go_up(idx_data, data):
parent_idx = self.get_parent_idx(idx_data)
self.dynamic_arr[idx_data] = self.dynamic_arr[parent_idx]
idx_data = parent_idx
self.dynamic_arr[idx_data] = data
# 우선순위가 높은 자식 노드의 인덱스를 반환
def which_is_prior_child(self, idx):
left_idx = self.get_left_child_idx(idx)
if left_idx > self.num_of_data:
return None
elif left_idx == self.num_of_data:
return left_idx
right_idx = self.get_right_child_idx(idx)
left_value = self.dynamic_arr[left_idx]
right_value = self.dynamic_arr[right_idx]
if self.get_prior(left_value, right_value) == -1:
return left_idx
else:
return right_idx
def is_go_down(self, idx, data):
child_idx = self.which_is_prior_child(idx)
if not child_idx:
return False
child_value = self.dynamic_arr[child_idx]
if self.get_prior(child_value, data) == -1:
return True
else:
return False
def delete(self):
if self.is_empty():
return None
ret_data = self.dynamic_arr[1]
last_data = self.dynamic_arr[self.num_of_data]
self.num_of_data -= 1
idx_data = 1
while self.is_go_down(idx_data, last_data):
child_idx = self.which_is_prior_child(idx_data)
self.dynamic_arr[idx_data] = self.dynamic_arr[child_idx]
idx_data = child_idx
self.dynamic_arr[idx_data] = last_data
self.dynamic_arr.pop()
return ret_data
if __name__ == "__main__":
heap = Heap("min")
heap.insert(3)
heap.insert(5)
heap.insert(1)
heap.insert(10)
heap.insert(8)
heap.insert(7)
heap.insert(4)
heap.insert(5)
heap.insert(2)
heap.insert(6)
heap.insert(9)
for i in range(1, heap.size()+1):
print(heap.dynamic_arr[i], end = ' ')
# 1 2 3 5 6 7 4 10 5 8 9
print("\n")
for i in range(1, heap.size()+1):
print(heap.delete(), end = ' ')
# 1 2 3 4 5 5 6 7 8 9 10
priority queue (우선순위 큐)
- 일반적인 큐는 FIFO 자료구조 이기 때문에 먼저 들어온 데이터를 먼저 내보냈다면, 우선순위 큐는 우선순위가 높은 데이터를 먼저 내보내는 자료구조
- 새로운 노드를 삽입하면 우선순위에 맞게 위치에 삽입 (Enqueue)
- 제거를 할 때는 가장 우선 순위가 높은 맨 앞에 노드를 빼면서 삭제(Dequeue)
class PriorityQueue(Heap):
enqueue = Heap.insert
dequeue = Heap.delete
if __name__ == "__main__":
pq = PriorityQueue("min")
pq.enqueue(3)
pq.enqueue(7)
pq.enqueue(2)
pq.enqueue(1)
pq.enqueue(9)
pq.enqueue(5)
pq.enqueue(8)
pq.enqueue(10)
pq.enqueue(5)
pq.enqueue(6)
pq.enqueue(4)
for i in range(1, pq.size()+1):
print(pq.dynamic_arr[i], end = ' ')
# 1 2 3 5 4 5 8 10 7 9 6
print("\n")
for i in range(1, pq.size()+1):
print(pq.dequeue(), end = ' ')
# 1 2 3 4 5 5 6 7 8 9 10

 초보몽키의 개발공부로그
초보몽키의 개발공부로그