패스트캠퍼스 컴퓨터공학 입문 수업을 듣고 중요한 내용을 정리했습니다. 개인공부 후 자료를 남기기 위한 목적임으로 내용 상에 오류가 있을 수 있습니다.

바이너리 서치 - 이진탐색 (binary search)

• BigO : O(log N)
• 정렬된 자료를 반으로 나누어 탐색하는 방법
• 주의점 : 자료는 오름차순 으로 정렬된 자료여야 한다.
• 이진트리, 바이너리서치는 코딩 인터뷰 단골문제
• 퍼포먼스가 아주 좋고 구현하는 중에 dynamic programming, recursion을 볼 수 있다.

특징

• linear search (순차검색) : 순서대로 찾는다. 성능평가시 비교대상으로 사용한다.
• linear search는 정렬 방식이 상관 없다.
• binary search (이진탐색) : 반드시 정렬된 상태에서 시작해야한다. 로그실행시간을 보장한다.
• 참고로 insert sort (삽입정렬), bubble sort, selection sort는 O(n^2)의 성능을 갖고 있다. (참고)

구현을 위한 준비

• target : 찾고자 하는 값
• data : 오름차순으로 정렬된 list
• start : data 의 처음 값 인덱스
• end : data 의 마지막 값 인덱스
• mid : start, end 의 중간 인덱스

구현 개요

• 자료의 중간 값이 (mid) 찾고자 하는 값인지 검사
• 아니라면 대소관계를 비교하여 start, end 값 이동
• 동일 연산 반복 (재귀로 구현 가능)

바이너리 서치 구현 (python)

# 바이너리 서치
# data 중에서 target 을 검색하여 index 값을 return 한다.
# 없으면 None을 return한다.

def binary_search(target, data):
    data.sort()
    start = 0
    end = len(data) - 1

    while start <= end:
        mid = (start + end) // 2

        if data[mid] == target:
            return mid # 함수를 끝내버린다.
        elif data[mid] < target:
            start = mid + 1
        else:
            end = mid -1

    return None

# 테스트용 코드
if __name__ == "__main__":
  li = [i**2 for i in range(11)]
  target = 9
  idx = binary_search(target, li)

  if idx:
      print(li[idx])
  else:
      print("찾으시는 타겟 {}가 없습니다".format(target))

바이너리 서치 재귀적 구현 (python)

# data는 오름차순으로 정렬된 리스트
def binary_search_recursion(target, start, end, data):
    if start > end:
        return None

    mid = (start + end) // 2

    if data[mid] == target:
        return mid
    elif data[mid] > target:
        end = mid - 1
    else:
        start = mid + 1        

    return binary_search_recursion(target, start, end, data)

# 테스트용 코드
if __name__ == '__main__':
    li = [i*3 for i in range(11)]
    target = 6
    idx = binary_search_recursion(target, 0, 10, li)

    print(li)
    print(idx)

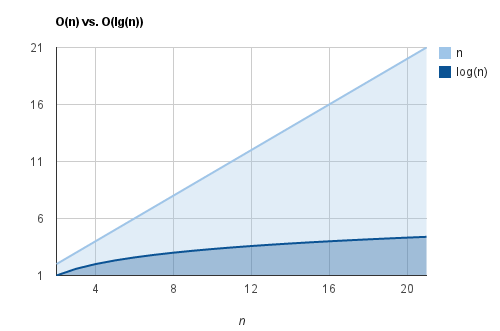
바이너리 서치 Big-0

• 참고자료
• 우선, 이진 탐색을 반복할수록 남아있는 (탐색할) 자료의 개수는 1/2로 줄어든다.
• 1번째 실행시 탐색할 남은 자료의 개수: N
• 2번째 실행시 탐색할 남은 자료의 개수: N/2
• 3번째 실행시 탐색할 남은 자료의 개수: N/2 * 1/2
• 4번째 실행시 탐색할 남은 자료의 개수: N/2 * 1/2 * 1/2
• K번째 실행시 탐색할 남은 자료의 개수: N*(1/2)^K
• 탐색이 끝나는 시점에는 남은 자료의 개수가 1이 되어야 한다. 따라서 N*(1/2)^K = 1
• 양 변에 2^K를 곱해주면 2^K = N > K = log2^N
• K의 의미는 실행횟수 따라서 자료의 갯수 N에 따른 시행횟수는 log2^N
  시간 복잡도는 BigO 표기법으로 O(logN) 으로 나타낼 수 있다.

참고자료

• 수업자료 - 바이너리서치
• 생활코딩 자료구조
• 인프런 알고리즘 강좌
• 참고강의 - Binary Search Tree

추가적으로 공부한 자료를 정리합니다.

바이너리 서치트리

• 자신의 값보다 작은 값은 왼쪽 자식 노드로, 자신의 값보다 큰 값은 오른쪽 자식 노드에 위치한다.

Node

• 트리는 노드의 구성체, 노드가 연결되어 트리가 된다.

class Node:
	def __init__(self, item):
		self.val = item
		self.left = None
		self.right = None

참고자료

• 바이너리 서치트리